终于补掉了KMP经久不衰的坑(雾
来写一下吧w
KMP可以用来解决一类字符串匹配问题。例如b串在a串中出现的次数。
那么具体是怎么实现的呢?通过“大跳”——next数组来实现。
这里先说一下next的定义:
$next[i]$表示$b[1…i]$中最长的相同前后缀(border)的长度。特别的,$next[1]=0$.
举个例子!
$b : “ABA”$
那么拿$next[3]$举例:
$b[1…3]$中最长相同的前后缀为$A$,长度为$1$,故$next[3]=1$.
怎么求出$next$数组呢?我会哈希!
显然,哈希也可以直接解决字符串匹配问题。那么既然是个算法,就一定有比$hash$巧妙的办法。
考虑把$next$数组按照类似于$dp$的方式递推转移(见下图)。

我们发现,计算$next[i]$本质上就是找到最长的两段红色序列,使得红色序列相等且下一个黄色也相等。
通俗的说,就是找一段$b[1…x]$,使得$b[1…x] = b[(x-1)-x+1 … (x-1)]$的同时还满足$b[x+1] = b[i]$.
然后有个很显然的东西:一个串的border的border一定是原串的border.
所以就往回一直跳就完事了。
1 | fail[1] = 0; |
那么如何用next数组优化找字符串呢?
考虑用一个指针$j$,指向目前匹配完了$b[j]$.
再次画图:
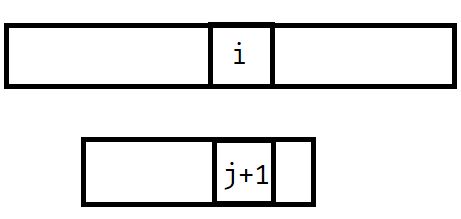
然后我发现我们通过固定i挪动j的位置,就可以合理匹配!
具体的,就是保证b串不回滚。由于我们已经匹配完了j个,那么跳个border一定还能匹配,就像这样:
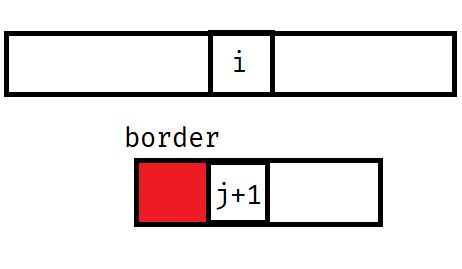
不停的跳,直到匹配或者确定不能匹配为止。
上代码:1
2
3
4
5
6
7
8
9
10for(int i = 1 , j = 0;i <= la;i++){
while(j && b[j + 1] != a[i]) j = fail[j];
if(b[j + 1] == a[i]){
j++;
}
if(j == lb){
++res;
j = fail[j]; // mark1
}
}
特别注意,有些题里找子串可以重复,有些题不能。如果不能的话,就把$mark1$处改成$j=0$. (重新开始)
那么KMP板子就写完了。附上luogu模板题代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41#include <iostream>
#include <cstdio>
#include <cstdlib>
//#include <algorithm>
#include <cstring>
#include <set>
#include <map>
#include <vector>
#define pb push_back
using namespace std;
const int MAXN = 1000000 + 10;
char a[MAXN] , b[MAXN];
static int fail[MAXN];
int main(){
scanf("%s%s" , (a + 1) , (b + 1));
int la = strlen(a + 1);
int lb = strlen(b + 1);
fail[1] = 0;
for(int i = 2;i <= lb;i++){
int j = fail[i - 1];
while(j && b[j + 1] != b[i]) j = fail[j];
if(b[j + 1] == b[i]) fail[i] = j + 1;
else fail[i] = 0;
}
for(int i = 1 , j = 0;i <= la;i++){
while(j && b[j + 1] != a[i]) j = fail[j];
if(b[j + 1] == a[i]){
j++;
}
if(j == lb){
cout << i - lb + 1 << "\n";
j = fail[j];
}
}
for(int i = 1;i <= lb;i++) cout << fail[i] << " ";
return 0;
}
exkmp好像可以直接用哈希+二分水过去…不学了(雾