虽然是个hash裸题但是KMP的做法也很妙~
答案就是$n-next[n]$.
为啥?
考虑画图。
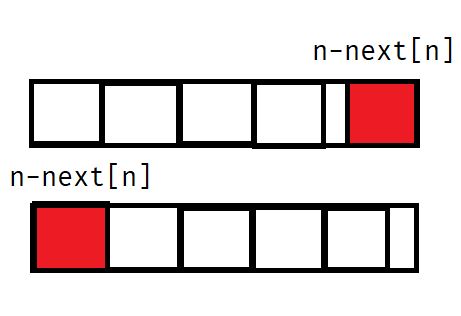
考虑根据$n-next[n]$的长度分段。
不难通过一一对应以及$border$的定义证明。
然后就完事了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34/**
* @Author: Mingyu Li
* @Date: 2019-03-16T09:53:21+08:00
* @Email: class11limingyu@126.com
* @Filename: P4391.cpp
* @Last modified by: Mingyu Li
* @Last modified time: 2019-03-16T09:55:56+08:00
*/
#include <bits/stdc++.h>
#define Go(i , x , y) for(register int i = x; i <= y; i++)
#define God(i , y , x) for(register int i = y; i >= x; i--)
typedef long long LL;
template < typename T > void sc(T& t) {
char c = getchar(); T x = 1; t = 0; while(!isdigit(c)) {if(c == '-') x = -1; c = getchar();}
while(isdigit(c)) t = t * 10 + c - '0' , c = getchar();t *= x;
}
template < typename T , typename... Args > void sc(T& t , Args&... args) {sc(t); sc(args...);}
const int N = 1000000 + 5;
char a[N];
int n , Next[N];
int main() {
sc(n); scanf("%s" , (a+1));
Next[1] = 0;
Go(i,2,n) {
int j = Next[i-1];
while(j && a[j+1] != a[i]) j = Next[j];
if(a[j+1] == a[i]) Next[i] = j+1;
else Next[i] = 0;
}
std::cout << n - Next[n] << "\n";
return 0;
}